Topics

Integration By Substitution Integration By Parts

Integration by Substitution

Intro

Consider the following integral:

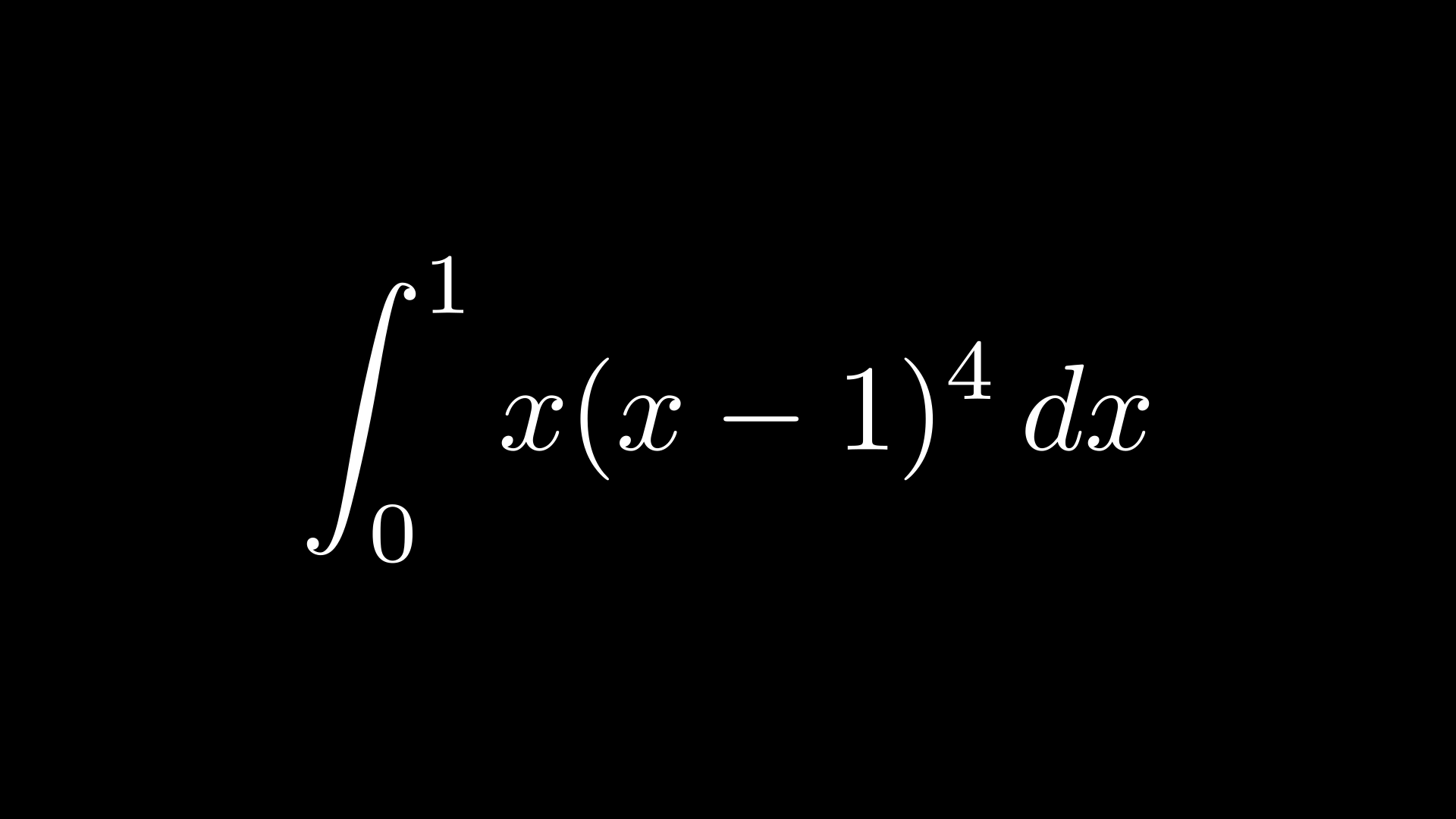
We could expand the binomial and integrate. However, we can consider a simple graph transformation, shifting the function one unit in the negative \(x\) direction (replacing \(x\) with \(x+1\) in the integrand and shifting the limits):

Here's a graphical view of what just happened, showing that the area we are finding hasn't changed:

Our new integral is therefore identical to the original integral as we have just shifted the function in the integral and the limits of the integral, to ensure we get the same area.

Now we can evaluate the integral, quite easily:

What we just did may not seem like much, but this is exactly how integration by substitution works. The goal of this technique is to transform the function we are trying to integrate to end up with a new function which is (hopefully) easier to integrate.

The formal method

Now we'll go through the same integral but using the formal method of substitution:

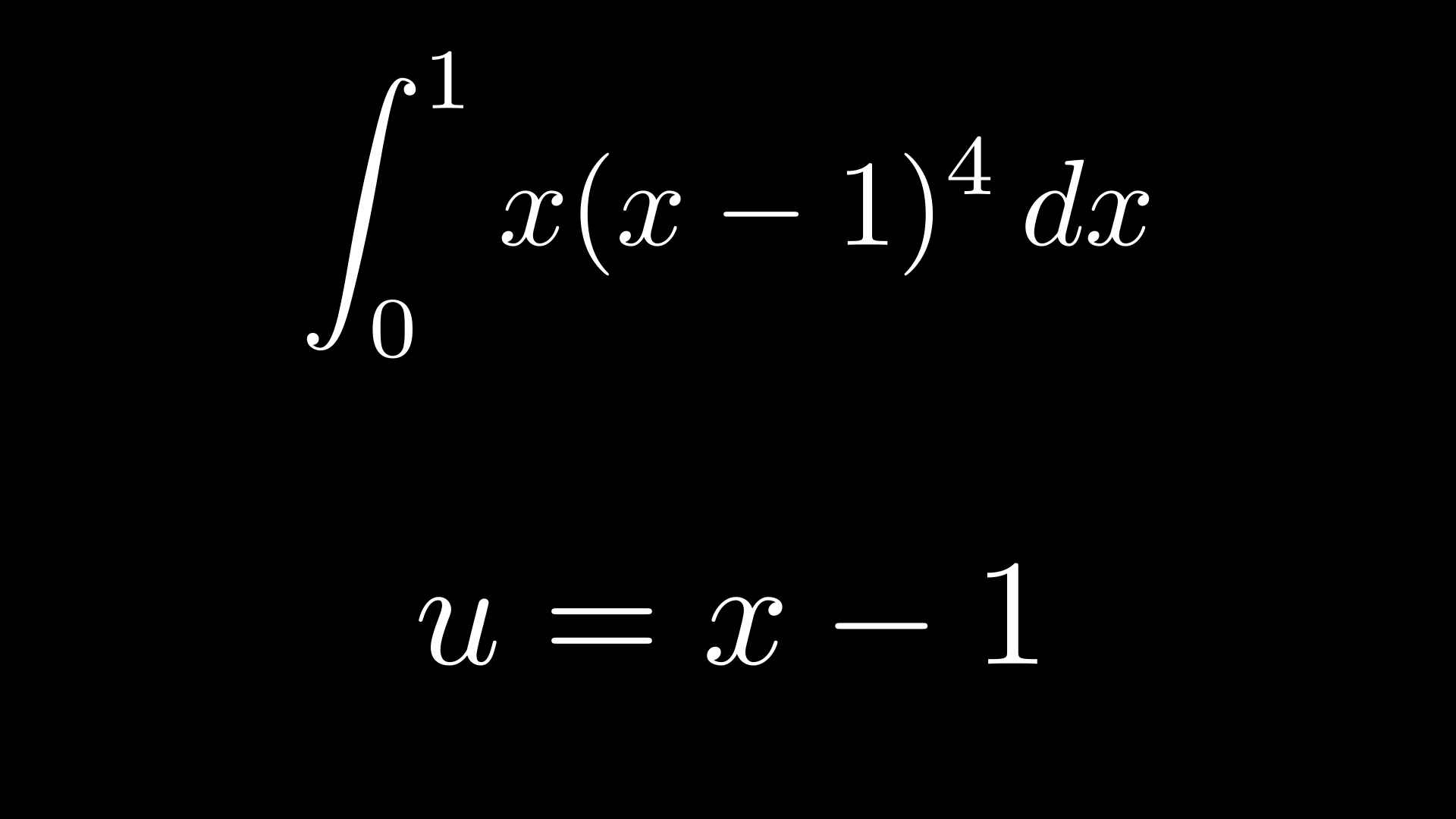
What's different now is that we introduce a new variable (u) rather than just replacing the \(x\) with \(x+1\). This helps distuinguish between the old and new integral and also helps for more advanced substitutions. We use this substitution in particular because it allows us to replace the pesky binomial \(x-1\) with a single variable to avoid binomial expansion.

Expressing the integrand in terms of u looks promising. But we cannot just replace the old integrand with this new one, as there are two problems:

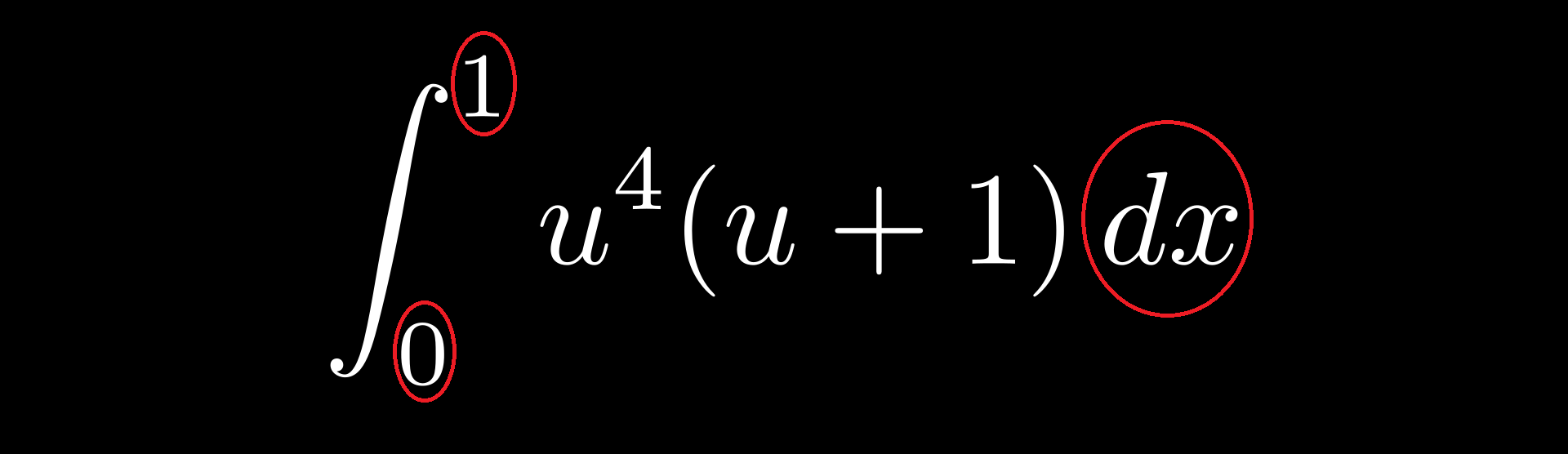
Our limits haven't been adjusted and we are still integrating with respect to x when our integrand is purely in terms of u. However, note that the limits correspond to when \(x = 0\) and \(x = 1\) respectively. We want our limits to be in terms of u as well, and thankfully we have an equation relating \(u\) with \(x\): \( u = x - 1 \). Subbing in \(x = 0\) and \(x = 1\) gives our new limits of \(u = -1\) and \(u = 0\) respectively.


Just one more step! We ideally want a \(du\) instead of \(dx\), so how can we find a relationship between \(du\) and \(dx\)? We use the fact that \(dx\) is an infinitely small change in \(x\). How do we relate a small change in \(u\) to a small change in \(x\)? We use differentiation:

Subbing in the \(dx\) for \(du\) gives us the same integral we got initially when considering the graph transformation.

One thing to point out is that we essentially treated \(du \over dx\) as a fraction to arrive at the result \(du = dx\). While the derivative behaves like a fraction, it is not exactly a fraction.   Here's why

Integration by Parts

Intro

It is important to first realise that if you've learnt the product rule, then this is nothing new. The integration by parts equation is merely a manipulation of the product rule, used to integrate a product of functions, and here's how:

Let \(f(x) = u(x)v(x)\):

Notice that the left hand side is the integral of the derivative of \(f(x)\), so we can simplify this:

We can now rewrite \(f(x)\) as \(u(x)v(x)\) and split the integral on the right hand side into 2 integrals:

A simple rearrangement of the equation leads to the integration by parts equation:

While this is just another representation of the product rule, the way we use this equation is quite different. To start, we must choose which of the 2 functions in the product must be \(u(x)\) and \(v'(x)\). To get to the right hand side of the above equation, we need to know what \(u'(x)\) and \(v(x)\) are. These can be found by differentiating \(u(x)\) and integrating \(v'(x)\) respectively.